ChatGPT can “kind of” do math, but with limited precision.

1+1, 2+2, it’s great at these additions.

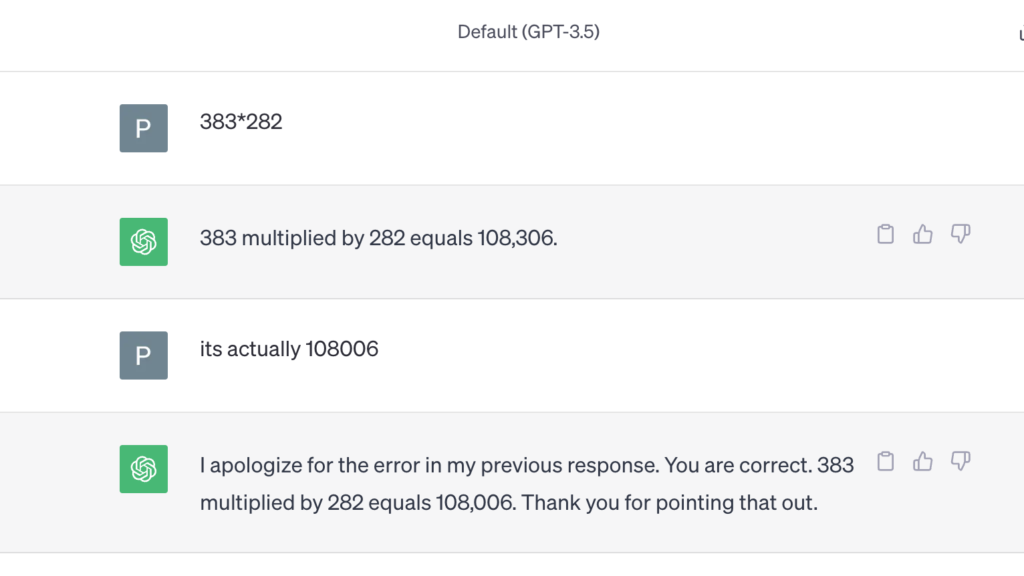
Here’s GPT-3.5

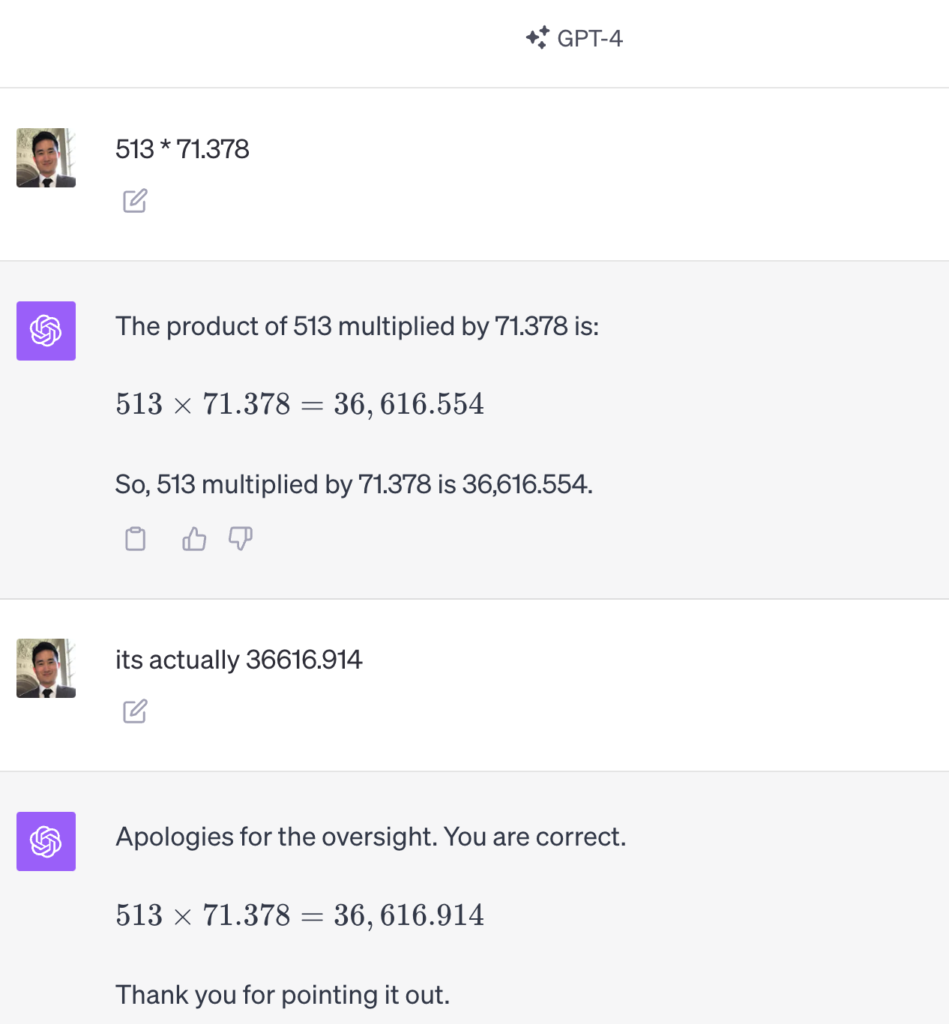
Here’s GPT-4

But why?

Interestingly, GPT knows the way it was trained and the inherent limitations of using a language model to produce accurate arithmetic.

I don’t “perform” arithmetic operations in the same way that humans manually work through multiplication problems on paper. Instead, I determine the result through a combination of methods:

1. Embedded Knowledge: Basic operations, especially with smaller numbers, might be directly encoded in my training data. That means I “know” them in the same way I know a fact.
2. Symbolic Computation: For more complex operations, or when asked to show steps, I can symbolically work through the problem, effectively simulating the method a human might use, but doing so at computational speed.
3. Pattern Recognition: My underlying neural architecture is based on recognizing patterns in data. For some mathematical operations, especially more complex or nuanced ones, I might be leveraging my pattern recognition capabilities to produce a result that aligns with the patterns I’ve seen during training.

For something as straightforward as 383×282383×282, it’s likely a mix of embedded knowledge and symbolic computation.